圆锥体积推导过程图解圆锥体积公式,推导过程

知识中心

您的位置：朵拉利品网 > 知识中心 > 圆锥体积推导过程图解圆锥体积公式,推导过程

2020-06-04 02:45:38 来源：朵拉利品网

1, 圆锥体积公式,推导过程

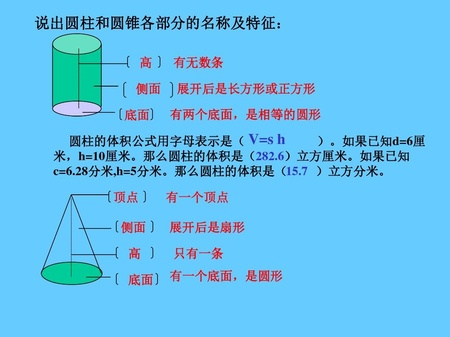
圆锥的体积
一个圆锥所占空间的大小，叫做这个圆锥的体积.
一个圆锥的体积等于与它等底等高的圆柱的体积的1/3
根据圆柱体积公式V=Sh(V=rrπh)，得出圆锥体积公式：
圆锥
V=1/3Sh
S是圆锥的底面积，h是圆锥的高，r是圆锥的底面半径。
证明：
把圆锥沿高分成k分每份高 h/k,
第 n份半径：n*r/k
第 n份底面积：pi*n^2*r^2/k^2
第 n份体积：pi*h*n^2*r^2/k^3
总体积（1+2+3+4+5+...+n）份：pi*h*(1^2+2^2+3^2+4^2+...+k^2)*r^2/k^3
因为
1^2+2^2+3^2+4^2+...+k^2=k*(k+1)*(2k+1)/6
所以
总体积（1+2+3+4+5+...+n）份：pi*h*(1^2+2^2+3^2+4^2+...+k^2)*r^2/k^3
=pi*h*r^2* k*(k+1)*(2k+1)/6k^3
=pi*h*r^2*(1+1/k)*(2+1/k)/6
因为当n越来越大，总体积越接近于圆锥体积，1/k越接近于0
所以pi*h*r^2*(1+1/k)*(2+1/k)/6=pi*h*r^2/3
因为V圆柱=pi*h*r^2
所以
V圆锥是与它等底等高的V圆柱体积的1/3

2, 圆锥体积公式的推导过程最容易理解的我是高一的学生请不要用微积分...

1.最直观的，做一个圆锥形容器和一个圆柱形容器，要求它们的底和高分别相等，
用圆锥装水向圆柱灌水，三次灌满，
可见，圆锥体积等于同底同高圆柱体积的1/3,
即V（圆锥）=πR^2h/3。
2.如果上面的太直观，显得没什么推导的技术含量，可参考下面的说法。
取一个四棱锥（底面是四边形的钉子状或楔子状的物体；一个面是四边形、另四个面是三角形的物体），
再取2个同样的四棱锥，可完整的拼成一个完整恰好的平行六面体（被拉斜了的长方体），
这个平行六面体的底面积与高与四棱锥相等，其体积为：底面积*高（上下底面的距离），
所以原来的四棱锥的体积为V=底面积*高/3。
而圆锥相当于底面变成了圆的无限多棱锥，因此类推，其体积也是等底等高的圆柱的1/3。

名词解释

棱锥

棱锥又称角锥，是三维多面体的一种，由多边形各个顶点向它所在的平面外一点依次连直线段而构成。多边形称为棱锥的底面。随着底面形状不同，棱锥的称呼也不相同，依底面多边形而定，例如底面是正方形的棱锥称为方锥，底面为三角形的棱锥称为三棱锥，底面为五边形的棱锥称为五棱锥等等。

圆锥

圆锥是一种几何图形，有两种定义。解析几何定义：圆锥面和一个截它的平面（满足交线为圆）组成的空间几何图形叫圆锥。立体几何定义：以直角三角形的直角边所在直线为旋转轴，其余两边旋转360度而成的曲面所围成的几何体叫做圆锥。旋转轴叫做圆锥的轴。垂直于轴的边旋转而成的曲面叫做圆锥的底面。不垂直于轴的边旋转而成的曲面叫做圆锥的侧面。无论旋转到什么位置，不垂直于轴的边都叫做圆锥的母线。（边是指直角三角形两个旋转边）

体积

体积，几何学专业术语，是物件占有多少空间的量。体积的国际单位制是立方米。一件固体物件的体积是一个数值用以形容该物件在三维空间所占有的空间。一维空间物件（如线）及二维空间物件（如正方形）在三维空间中都是零体积的。