求三角形斜边长勾股 求三角形斜边长公式

2020-05-24 21:07:27 来源：朵拉利品网

1, 求三角形斜边长公式

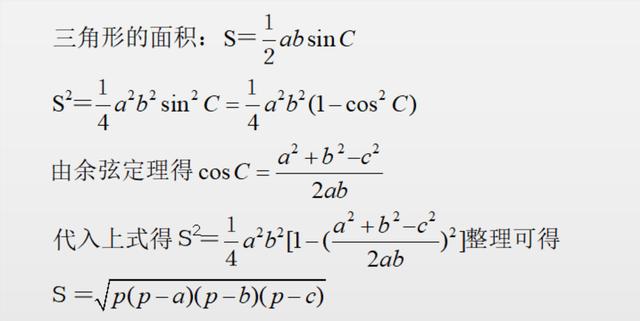
已知底边1.15米。高度0.3米，可以根据勾股定理公式来计算：
（斜边是直角三角形才有，指直角对应的那一条边，直角的两个边叫直角边）
设直角三角形两直角边长为a、b，斜边长为c:
a^2+b^2=c^2（勾股定理）
公式：直角边的平方+直角边的平方=斜边的平方
则 c=√（a^2+b^2） （√表示根号）
将a=3.8,b=1.2代入，解得：
c=√15.88≈3.985m （≈表示约等号）
三角斜边的定理：
1、直角三角形底边上的中线等于斜边的一半，直角三角形斜边上的中线等于斜边的一半。
2、在直角三角形中，如果有一个锐角等于30°，那么它所对的直角边等于斜边的一半。
3、在直角三角形中，如果有一条直角边等于斜边的一半，那么这条直角边所对的锐角等于30°。
4、在直角三角形中，两条直角边a、b的平方和等于斜边c的平方，即a2+b2=c2。
5、（h为斜边上的高），外接圆半径斜边上的中线，内切圆半径。
参考资料来源：搜狗百科-勾股定理

2, 三角形斜边长怎么算

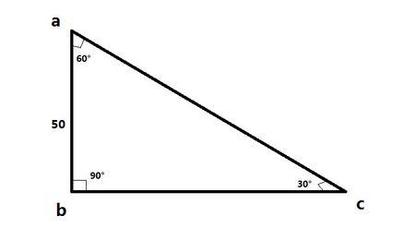
c（斜边）=√（a²+b²）。（a,b为两直角边）
解答过程如下：
(1)在直角三角形中满足勾股定理—在平面上的一个直角三角形中，两个直角边边长的平方加起来等于斜边长的平方。数学表达式：a²+b²=c²
(2)a²+b²=c²求c，因为c是一条边，所以就是求大于0的一个根。即c=√（a²+b²）。
直角三角形特殊性质
它除了具有一般三角形的性质外，具有一些特殊的性质：
1、直角三角形两直角边的平方和等于斜边的平方。如图，∠BAC=90°，则AB²+AC²=BC²（勾股定理）
2、在直角三角形中，两个锐角互余。如图，若∠BAC=90°，则∠B+∠C=90°
3、直角三角形中，斜边上的中线等于斜边的一半（即直角三角形的外心位于斜边的中点，外接圆半径R=C/2）。该性质称为直角三角形斜边中线定理。
4、直角三角形的两直角边的乘积等于斜边与斜边上高的乘积。
参考资料来源：百度百科-直角三角形

3, 直角三角形求斜边长计算公式

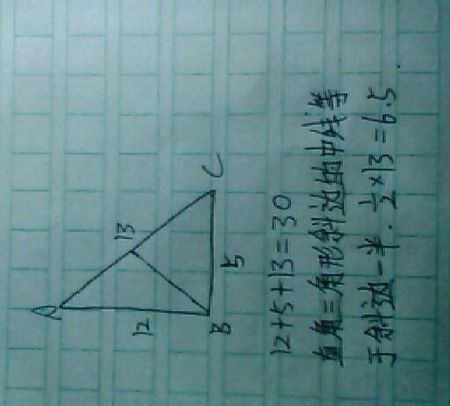
如果是直角三角形的话，建议使用勾股定理
勾股定理是一个基本的初等几何定理，直角三角形两直角边的平方和等于斜边的平方。如果直角三角形两直角边为a和b，斜边为c，那么a²+b²=c²，若a、b、c都是正整数，（a,b,c）叫做勾股数组。
勾股定理现约有500种证明方法，是数学定理中证明方法最多的定理之一。勾股定理是人类早期发现并证明的重要数学定理之一，用代数思想解决几何问题的最重要的工具之一，也是数形结合的纽带之一。“勾三，股四，弦五”是勾股定理的一个最著名的例子。
远在公元前约三千年的古巴比伦人就知道和应用勾股定理，还知道许多勾股数组。古埃及人也应用过勾股定理。在中国，西周的商高提出了“勾三股四弦五”的勾股定理的特例。在西方，最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯，他用演绎法证明了直角三角形斜边平方等于两直角边平方之和。

名词解释

斜边

斜边是指直角三角形中最长的那条边，也指不是构成直角的那条边。在勾股定理中，斜边称作“弦”。

直角

《几何原本》中的定义：当一条直线和另一条横的直线交成的邻角彼此相等时，这些角的每一个被叫做直角，而且称这一条直线垂直于另一条直线。角度比直角小的称为锐角，比直角大而比平角小的称为钝角。

直角三角形

直角三角形是一个几何图形，是有一个角为直角的三角形，有普通的直角三角形和等腰直角三角形两种。 其符合勾股定理，具有一些特殊性质和判定方法。

• 上一篇 怎样算三角形的斜边长 怎么算出三角形斜边长度？
• 下一篇 前斜边的英语是什么 直角三角行英文是什么以及斜边直角边的英文