直角三角形的中线有什么特点 直角三角形斜边上的中线有什么特性？

2020-05-24 21:03:47 来源：朵拉利品网

1, 直角三角形斜边上的中线有什么特性？

三角形中线是一边中点和一个顶点的连线，有三条，三条中线交于一点，这个点叫三角形的重心。重心分中线的比为
2:1 。
三条内角平分线也交于一点，叫三角形的内心，也是三角形内接圆的圆心。内心到三角形三边的距离相等。也可以由正弦定理得到内、外角平分线定理。（内角：在三角形ABC中，当AD是顶角A的角平分线交底边于D时，BD/CD=AB/AC
外角：在三角形abc中，当角A的外角平分线交BC的延长线于D时，BD/CD=AB/AC）
两条外角平分线与一条内角平分线交于一点，叫三角形的离心.三角形有三个离心.

2, 直角三角形斜边中线有啥特征？

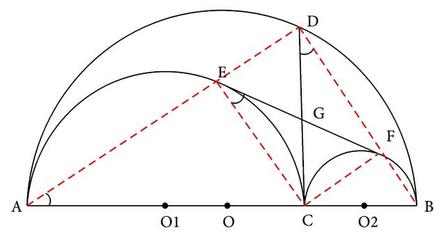
定理内容编辑
定理：如果一个三角形是直角三角形，那么这个三角形斜边上的中线等于斜边的一半。
逆命题编辑
其逆命题1：如果一个三角形一条边的中线等于这条边的一半，那么这个三角形是直角三角形，且这条边为直角三角形的斜边。
逆命题1是正确的。以该条边的中点为圆心，以中线长为半径作圆，则该边成为圆的直径，该三角形的另一个顶点在圆上，该顶角为圆周角。因为直径上的圆周角是直角，所以逆命题1成立。
原命题2：如果CD是直角三角形ABC斜边AB上的中线，那么它等于AB的一半。
逆命题2：如果线段BD的一端B是直角三角形ABC的顶点，另一端D在斜边AC上，且BD等于AC的一半，那么BD是斜边AC的中线。

名词解释

逆命题

逆命题是指对于两个命题，如果一个命题的条件和结论分别是另外一个命题的结论和条件，那么这两个命题叫做互逆命题，其中一个命题叫做原命题，另外一个命题叫做原命题的逆命题。

斜边

斜边是指直角三角形中最长的那条边，也指不是构成直角的那条边。在勾股定理中，斜边称作“弦”。

直角三角形

直角三角形是一个几何图形，是有一个角为直角的三角形，有普通的直角三角形和等腰直角三角形两种。 其符合勾股定理，具有一些特殊性质和判定方法。

• 上一篇 直角三角形斜边公式 三角形斜边计算公式
• 下一篇 斜边英语单词 斜边用英语怎么说