直角三角形斜边中线的逆定理 直角三角形斜边中线的逆定理怎么证,两种方法

2020-05-24 20:55:36 来源：朵拉利品网

1, 直角三角形斜边中线的逆定理怎么证,两种方法

直角三角形斜边中线等于斜边的一半。
设在直角三角形ABC中，∠BAC=90°，AD是斜边BC的中线，求证：AD=1/2BC。
【证法1】
延长AD到E，使DE=AD，连接CE。
∵AD是斜边BC的中线，
∴BD=CD,
又∵∠ADB=∠EDC（对顶角相等），
AD=DE,
∴△ADB≌△EDC(SAS),
∴AB=CE，∠B=∠DCE,
∴AB//CE（内错角相等，两直线平行）
∴∠BAC+∠ACE=180°（两直线平行，同旁内角互补）
∵∠BAC=90°，
∴∠ACE=90°，
∵AB=CE，∠BAC=ECA=90°，AC=CA,
∴△ABC≌△CEA(SAS)
∴BC=AE,
∵AD=DE=1/2AE,
∴AD=1/2BC。
取AC的中点E，连接DE。
∵AD是斜边BC的中线，
∴BD=CD=1/2BC,
∵E是AC的中点，
∴DE是△ABC的中位线，
∴DE//AB（三角形的中位线平行于底边）
∴∠DEC=∠BAC=90°（两直线平行，同位角相等）
∴DE垂直平分AC,
∴AD=CD=1/2BC（垂直平分线上的点到线段两端距离相等）。
延长AD到E，使DE=AD，连接BE、CE。
∵AD是斜边BC的中线，
∴BD=CD,
又∵AD=DE,
∴四边形ABEC是平行四边形（对角线互相平分的四边形是平行四边形），
∵∠BAC=90°，
∴四边形ABEC是矩形（有一个角是90°的平行四边形是矩形），
∴AE=BC（矩形对角线相等），
∵AD=DE=1/2AE,
∴AD=1/2BC。

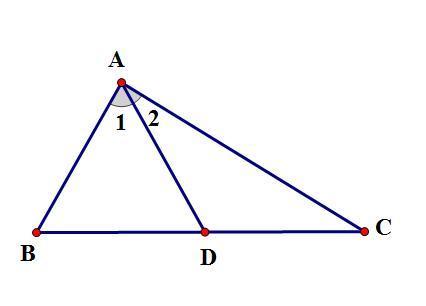
【直角三角形斜边中线等于斜边的一半有逆命题，但证明题不能直接运用】
逆命题为：【如果三角形的一边中线等于该边长的一半，那么三角形为直角三角形。】
设在△ABC中，AD为BC边的中线，且AD=1/2BC，求证：△ABC为直角三角形。
证明过程：
∵AD是BC边的中线，
∴BD=CD=1/2BC,
∵AD=1/2BC,
∴BD=AD=CD,
∴∠1=∠B，∠2=∠C,
∴∠1+∠2=∠B+∠C,
即∠BAC=∠B+∠C,
∵2∠BAC=∠BAC+∠B+∠C=180°（三角形内角和180°），
∴∠BAC=90°，
∴△ABC是直角三角形。
直角三角形的性质：
1、直角三角形两直角边的平方和等于斜边的平方。如图，∠BAC=90°，则AB²+AC²=BC²（勾股定理）
2、在直角三角形中，两个锐角互余。如图，若∠BAC=90°，则∠B+∠C=90°
3、直角三角形中，斜边上的中线等于斜边的一半（即直角三角形的外心位于斜边的中点，外接圆半径R=C/2）。该性质称为直角三角形斜边中线定理。
4、直角三角形的两直角边的乘积等于斜边与斜边上高的乘积。
5、在直角三角形中，如果有一个锐角等于30°，那么它所对的直角边等于斜边的一半。

名词解释

AD

广告（advertisement）意思为广而告之，是指向社会广大公众告知某件事情或某个事物，就其含义而言，有广义和狭义之分。广义广告是指不以营利为目的的广告，如政府公告，政党、宗教、教育、文化、市政、社会团体等方面的启事、声明等。狭义广告是指一种市场营销行为，即商业广告，它是工商企业为推销商品或提供服务，以付费方式通过广告媒体向消费者或用户传播商品或服务信息的手段。

DE

沙漠之鹰是1980年由MRI发布的一部狩猎手枪。原型枪则在1981年完成，而最终定型则是在以色列军事工业公司（IMI）。第一把具有完全功能的0.357口径的手枪问世后成为了收藏家和枪械爱好者疯狂追逐的对象。

90

90（九十）是89与91之间的一个自然数，也是一个偶数。该数除了本身之外，其他约数的和为144>90，因此它是过剩数（盈数）。

• 上一篇 直角三角形斜边中线定理 怎么证明定理直角三角形斜边上的中线等于斜边的一半
• 下一篇 小学生直角三角形斜边怎么算 直角三角形斜边怎么算