声压级和分贝关系 声级和声压级的区别?
2020-04-13 04:36:57
来源:朵拉利品网
1, 声级和声压级的区别?

声级是一个物理量,声压级是算是一个数值。声压级以符号SPL表示,其定义为将待测声压有效值p(e)与参考声压p(ref)的比值取常用对数,再乘以20,即:SPL=20LOG(10)[p(e)/p(ref)]。一般讲,低于这一声压值,人耳就再也不能觉察出这个声音的存在了。显然该可听阈声压的声压级即为零分贝。声级是指与人们对声音强弱的主观感觉相一致的物理量,单位为分贝。听闻对应的声级为0分贝,但0分贝并不意味着没有声音,而是可闻声的起点,声强每增加10分贝,其声级就增加10分贝,房间的本底噪声的声级大约为40分贝,正常对话为70分贝,交响乐高潮时为90分贝,人的痛阈声级为120分贝。声级:近似于人耳对声音各频率成分感觉程度综合成的总声压级数值。是声音经过声级计中根据人耳对声音各频率成分的灵敏度不同而设计的计权网络(特殊电路)修正过的总声压级值。单位为分贝,其数值因所用的计权网络而异,所以应注明所用的计权网络符号。一般常用A计权测量,其结果则以分贝A表示。
2, 按声强级和声压级的定义,对同一个声音两者的分贝值是否相等?

声强级定义:L=10lg(a/b) a为要表示的声强,即为声功率单位是W.m-2.瓦每平方米b为基准声强,为人耳感知最小声强,大小为10exp-12。10的负12次方例如a=10exp-6,10的负六次方,带公式即为,60dB。声压级定义:L=20lg(c/d) c为要表示的声压,单位为pa。d为基准声压,为人耳感知的最小声压,大小为2*10exp-5。2乘以10的负五次 方。例如,c=2*10exp-2,2乘以10的负二次方。带入得L=60dB。自由声场,声强和声压关系为I=P2/(C*q) I为声强,P为声压,C为声速,q为空气密度,2为平方可以换算一下,上述两个声强,声压级是相等的。而声压级lg前面的2正说明了,声强与声压平方成正比。但这是理想情况,即声音在大气中传播,可以忽略大气温度,压力变化情况下,两个级是相等的。因为大气参数变化,声压声强的关系式会发生变化。基准声压,声强不在对应。所以会有略微的差别。但只要不是研究苛刻的实际问题,二者数值上没有区别,是相等的。
3, 请问声压与声压级的区别?
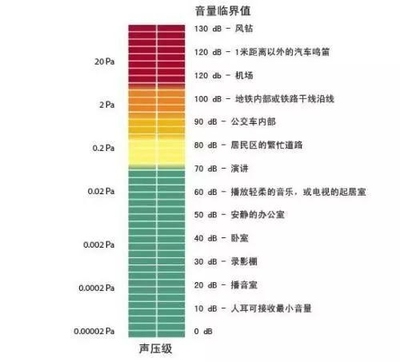
1、定义不同声压:声压就是大气压受到声波扰动后产生的变化,即为大气压强的余压,它相当于在大气压强上的叠加一个声波扰动引起的压强变化。由于声压的测量比较容易实现,通过声压的测量也可以间接求得质点速度等其它物理量,所以声学中常用这个物理量来描述声波。声压级:给定声压与参考声压之比的以10为底的对数乘以20,以分贝计。在空气中参考声压p(ref)一般取为2*10E-5帕,这个数值是正常人耳对1千赫声音刚刚能觉察其存在的声压值,也就是1千赫声音的可听阈声压。一般讲,低于这一声压值,人耳就再也不能觉察出这个声音的存在了。显然该可听阈声压的声压级即为零分贝。2、产生原因不同声压:介质压强的变化量称为声压。介质中有声场时的压强P与没有声场时的压强P0之差即为声压。由于声压的测量比较容易实现,通过声压的测量也可以间接求得质点速度等其它物理量,所以声学中常用这个物理量来描述声波。声压级:从听阈到痛阈,声压的绝对值相差1000000倍。显然,用声压的绝对值表示声音的大小是不方便的。为了便于应用,人们便根据人耳对声音强弱变化响应的特性,引出一个对数量来表示声音的大小,这就是声压级。声压:声压的单位是帕斯卡(pa),其计算公式为:声压(p)的平方=声强(I)*介质密度(ρ)*声速(C)其中,声强单位是:W/m2 密度单位:kg/m3 声速:m/s声压级:声压级以符号SPL表示,其定义为将待测声压有效值p(e)与参考声压p(ref)的比值取常用对数,再乘以20,即:SPL=20LOG(10)[p(e)/p(ref)]其单位是分贝。参考资料来源:搜狗百科-声压参考资料来源:搜狗百科-声压级
名词解释
声强
定义:声波平均能流密度的大小叫声强。声强对面积积分,则为单位时间内通过一定面积的的声波能量,因具有功率的单位,又叫做声功率。声功率通常还很小,一个人说话的声功率仅约10^-5W,故一千万人同时说话,也只100W。人们发声所消耗的能量绝大部分均转化为其他形式例如热运动的能量,用于发声的仅约1%
声压
声压就是大气压受到声波扰动后产生的变化,即为大气压强的余压,它相当于在大气压强上的叠加一个声波扰动引起的压强变化。由于声压的测量比较容易实现,通过声压的测量也可以间接求得质点速度等其它物理量,所以声学中常用这个物理量来描述声波。英文名:sound pressure。
相关资讯
最新资讯
