转轴的转动惯量 圆环 转轴沿直径的转动惯量如何推导？

2019-07-21 21:02:04 来源：朵拉利品网

1, 圆环 转轴沿直径的转动惯量如何推导？

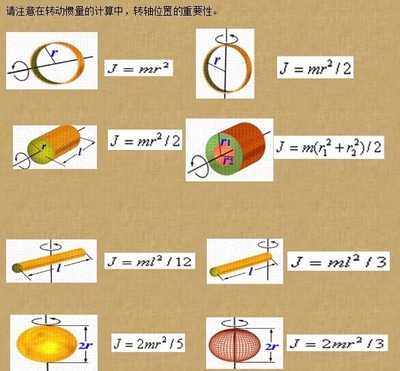
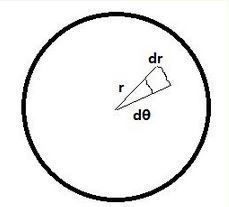
通过圆环中心轴推出。
首先要理解什么是薄圆环，所谓薄圆环指的是径向厚度趋近于零，也就是内径和外径无限接近。
也就是内外径近似可以看做一个定值：R
则：沿圆周的线密度：ρ=m/2πR
沿圆周的方向取Δθ，
由：J=mR^2
则有：ΔJ=R^2dm
dm=(m/2πR)Rdθ
故有：dJ=R^2dm=R^2(m/2πR)Rdθ=（R^2m/2π）dθ
两边积分，积分区间[0,2π]：J=2π（R^2m/2π）=R^2m
通过圆环直径轴。
取角度为：θ处的任意小的角度：Δθ，θ为转轴与直径的夹角。
则有：dJ=(Rcosθ)^2dm=(Rcosθ)^2(m/2πR)Rdθ=R^2(cos2θ+1)^2mdθ/4π
两边积分，积分区间为：[0,2π]：J=(mR^2sin2θ)/2+mR^2/2=0+mR^2/2=mR^2/2

2, 圆盘的转动惯量

薄圆盘的转动惯量的计算公式
当回转轴通过中心与盘面垂直时，
转动惯量（Moment of Inertia）是刚体绕轴转动时惯性（回转物体保持其匀速圆周运动或静止的特性）的量度，用字母I或J表示。
在经典力学中，转动惯量（又称质量惯性矩，简称惯距）通常以I 或J表示，SI 单位为 kg·m²。对于一个质点，I = mr²，其中 m 是其质量，r 是质点和转轴的垂直距离。

3, 电机的转动惯量是什么意思

转动惯量是指物体绕某一轴的转动，一般来说绕x轴转动用Ix表示。
转动惯量定义为：J=∑ mi*ri^2
(1)式中mi表示刚体的某个质点的质量，ri表示该质点到转轴的垂直距离。
转动惯量是表征刚体转动惯性大小的物理量，它与刚体的质量、质量相对于转轴的分布有关。
刚体的转动惯量是由质量、质量分布、转轴位置三个因素决定的。
(2)同一刚体对不同转轴的转动不同，凡是提到转动惯量，必须指明它是对哪个轴的才有意义。

相关概念

转动惯量

转动惯量(Moment of Inertia)是刚体绕轴转动时惯性（回转物体保持其匀速圆周运动或静止的特性）的量度，通常以/或J表示。 在经典力学中，转动惯量（又称质量惯性矩，简称惯距）通常以/或J表示，SI 单位为 kg·m²。对于一个质点，/=mr²，其中 m 是其质量，r是质点和转轴的垂直距离。转动惯量在旋转动力学中的角色相当于线性动力学中的质量，可形式地理解为一个物体对于旋转运动的惯性，用于建立角动量、角速度、力矩和角加速度等数个量之间的关系。

刚体

刚体（rigid body）是一种有限尺寸，可以忽略形变的固体。 在这篇文章内，矢量与标量分别用粗体与斜体显示。例如，位置矢量通常用正在加载表示；而其大小则用正在加载来表示。 不论是否感受到外力，在刚体内部，质点与质点之间的距离都不会改变。这种理想模型适用条件是，运动过程比固体中的弹性波的传播要缓慢得多。根据相对论，这种物体不可能实际存在，但物体通常可以假定为完美刚体，前提是必须满足运动速度远小于光速的条件。 在经典力学里，刚体通常被视为连续质量分布体；在量子力学里，刚体被视为一群粒子的聚集。例如，分子（由假定为质点的电子与核子组成）时常会被视为刚体。

转轴

转轴、笔记本转轴等，顾名思义即是链接产品零部主件必须用到的、用于转动工作中既承受弯矩又承受扭矩的轴称为转轴。常见的转轴有：手机转轴（翻盖或旋转屏手机）；笔记本电脑转轴；便携式DVD转轴；LED台灯转轴；LCD显示屏转轴；GPS等车载支架转轴等

• 上一篇 手机线转轴厂家 关于手机问题
• 下一篇 手机转轴特点 手机内部结构